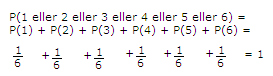|
||||||||||||
 HJEM HJEM |
||||||||||||
| 20. Sannsynlighet | ||||||
|
20. 1. Innledning | 20. 2. Utfallsrom | 20. 3. Eksperimentell sannsynlighet - relativ frekvens - hyppighet | 20. 4. Teoretisk sannsynlighet | 20. 5. Uniform sannsynlighet | 20. 6. Komplementære hendelser | 20. 7. Produktsetningen for uavhengige hendelser | 20. 8. Telleregler Hendelser som kan forutsies kalles deterministiske. Hendelser vi ikke kan forutsi, som for eksempel terningkast, kalles tilfeldige forsøk.
Hvor mange utfall kan et terningkast ha? En terning har øyner fra en til seks, det betyr at utfallet vil være blant disse. Vi kaller alle mulige utfall for utfallsrommet. Et enkelt utfall vil være et element i utfallsrommet:
U = { 1, 2, 3, 4, 5, 6 }
Hva er sjansen for å få fire øyner? Vi kan finne det ut på to måter, ved å gjennomføre mange terninkast, og ved regning. 20. 3. Eksperimentell sannsynlighet - relativ frekvens - hyppighet Vi lar datamaskinen kaste terning for oss, det kalles å simulere terningkast. På 20 kast får maskinen hele 6 firere. Den relative frekvensen for firerer etter 20 kast er 6/20 = 0,3 eller 30%. Figur 1. viser fordelingen av øyner.
Figur 1.: Figuren viser fordelingen av øyner etter 20 terninkast. Ut fra erfaring vil man kanskje forvente at sannsynligheten for å få firere og femere skulle være den samme, siden terninger normalt har en side som gir fire øyner og en side som gir fem øyner. Etter 20 terningkast kan man ikke trekke en slik konklusjon.
Vi setter maskinen til å kaste en terning 10.000 ganger. Det gir følgende resultat: 
Figur 2.: Figuren viser fordelingen av øyner etter 10000 terninkast.
Nå ser det ut til at sannsynligheten for fire øyner går mot et tall som ligger rundt 0,16 – 0,17, dvs. 16 – 17%. Man ser at sannsynliheten for å få et annet antall øyner er nesten den samme.
Sannsynligheten er lik den relative frekvens i det lange løp. Nå er ikke 10.000 det samme som "det lange løp", men tilstrekkelig til å se en tendens som bekreftes når vi behandler problemet teoretisk.
Utfallsrommet viser oss at det er seks mulige utfall når vi kaster en terning. Vi er bare interessert i å få en firer. Bare en av seks muligheter gir en firer. Det betyr at sannsynligheten for å få en firer i et kast er 1/6 eller 0,167 eller 16,7%. Vi kan skrive det slik: P (4) = 1/6 = 0,167 = 16,7% Dersom du lurer på skrivemåten P(4) – Hvorfor brukes bokstaven P og ikke S for sannsynlighet? P står for det engelske probability som betyr noe i nærheten av sannsynlighet, derfor P. Sannsynligheten kan altså presenteres som
Presentasjonsformene er likeverdige. Man forutsetter at sannsynligheten for å få et av de seks utfallen er den samme for alle utfall. Når det er slik sier vi at vi har en uniform sannsynlighet. Om våre teoretiske sannsynlighetsmodeller er gode, er det kun utprøving som kan fortelle oss.
Når vi har en uniform sannsynlighetsmodell er sannsynligheten for en hendelse gitt ved:
Når modellen er uniform er sannsynligheten for at et hvilket som helst element i utfalsrommet skal bli utfallet, den samme. Hva er sannsynligheten for å få en femmer eller en sekser i et terningkast? Sannsynligheten for å få en femmer er 1/6 og sannsynligheten for å få en sekser er 1/6. Sannsynligheten for femmer eller sekser blir da: Hva er så sannsynligheten for å få 1, 2, 3, 4, 5 eller 6? Det blir: Terningen måtte lande på et av disse antall øyner, derfor var det helt sikkert at vi ville få et av utfallene.
20. 6. Komplementære hendelser Dersom vi kaller sannsynligheten for å få 6 for P(A), vil sannsynligheten for ikke å få 6 være P(A*). Vi har da følgende relasjon:
Hendelser som ikke er A skrives A*. Utfallsrommet kan illustreres slik: Eks: I en klasse er det noen elever som spiller fotball på fritiden. Disse er A. De som ikke spiller fotball er A*.
Sannsynligheten for å trekke ut en elev som ikke spiller fotball blir P(ikke fotball) = 12/(12+6) = 12 /18 = 2/3, eller ca. 67%
20. 7. Produktsetningen for uavhengige hendelser To hendelser er uavhengige dersom utfallet av den første hendelsen ikke påvirker utfallet av den andre hendelsen. Eksempel: Dersom du kaster en terning to ganger vil ikke resultastet fra første kast ha noen innvirkning på utfallet i andre kast. Dersom hendelsen A og B er uavhengige, er P( A og B) = P(A) ∙ P(B) Eksempel: Hva er sannsynligheten for at du får to seksere når du kaster en terning to ganger? P( 6 og 6) = P(6) ∙ P(6) = (1/6) ∙ (1/6) = 1/36
Dersom en situasjonen består av flere trinnvise valg mellom flere elementer blir antall kombinasjoner som følger.:
Antall elementer i første valgrunde multiplisert med antall elementer i andre runde osv. m ∙ n ∙ …..
Eks 1.:
Hvor mange antrekk kan du velge dersom du har valget mellom to gensere, fire bukser og tre par sko? Svar: 2 (gensere) ∙ 4 (bukser) ∙ 3 (par sko) = 24 (antrekk) Eks. 2.: Hvor mange forskjellige menyer kan komponeres av tre forretter, fire hovedretter og seks desærer? Svar: 3 ∙ 4 ∙ 6 = 72 |
||||||
© 2000- 2024 Sivilingeniør Kenneth Marthinsen, org. no: 976 773 934.
Telefon 932 99 111 Postadr. Odvar Solbergs vei 112, 0973 OSLO
MAIL OSS
|
|
||