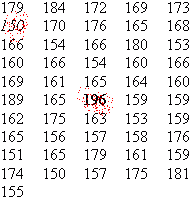|
||||||||||||
 HJEM HJEM |
||||||||||||
| 19. Statistikk | ||||
|
19.1. Innledning | 19. 2. Frekvenstabell | 19. 3. Søylediagram | 19. 4. Gjennomsnitt | 19. 5. Median | 19. 6. Typetall | 19. 7. Vurdering | 19. 8. Histogram | 19. 9. Klassebredde | 19.10. Variasjonsbredde | 19. 11. Sektordiagram Statistikk er å bearbeide tallmaterialet / data slik at vi forhåpentligvis kan observere en trend eller tendens. I beste fall kan vi trekke en konklusjon. Tallmaterialet skaffes ofte ved hjelp av spørreundersøkelser, målinger eller observasjoner. Statistikk kan presenteres i forskjellige former og det kan være en god måte å speile virkeligheten på.
Statistikk kan også, uten å være direkte feil, presenteres på en måte som tåkelegger virkeligheten. I slike tilfeller er det ofte interessegrupper som presenterer et tallmaterialet med det formål å fremme sin sak. VÆR PÅ VAKT, i slike tilfeller er statistikk mer forvirrende en forklarende.
Eksempel 1:
En liten skoleklasse har ti elever. Vi spør hvor mange søsken hver enkelt har. Svarene vi får er følgende: 2, 3, 1, 5, 5, 3, 3, 1, 3, 1 Vi kan sette resultatet opp i en tabell: Med frekvens mener vi hvor mange ganger et svar forekommer. Tabellen kan presenteres som den er, eller vi kan presentere den som et diagram. Et eksempel kan være et søylediagram. På y aksen har vi antall observasjoner og på x aksen har vi de forskjellige type observasjoner. Gjennomsnitt er summen av alle verdier delt på antall verdier.
Eksempel 2:
Median er den midterste verdien etter alle verdien er blitt sortert i stigende rekkefølge. Dersom antall verdier er parttall (2,4,6.....) er median gjennomsnittet av de to midterste verdiene.
Eksempel 3:
Datamengden er 10, et parttall. Median blir gjennomsnittet av 3 og 3 som er (3+3)/2=3 Typetallet er den verdi som det er flest forekomster av i datamengden. I vårt eksempel er typetallet 3, fordi det forekommer flest (4) ganger. Som dere ser har vi tre forskjellige mål for sentraltendens. Målene kan gi forskjellige verdier. Det er viktig at man vurdere hvilket mål man finner mest hensiktsmessig å bruke i hvert enkelt tilfelle. Vi måler høyden på alle 15-åringer i idrettslaget. Det er 51 stykker. Her er resultatet i cm:
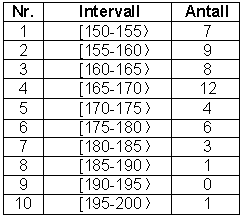
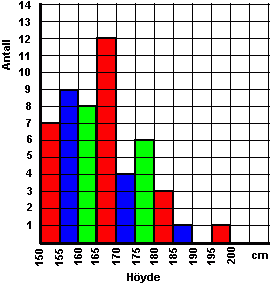
Vi grupperer medlemmene på den måten at vi sier at alle med høyde mellom for eksempel 160cm og 165cm representerer en søyle. Alle mellom 165cm og 170cm en annen søyle, osv. Vi lager intervaller som også kalles klasser. I dette eksemplet er intervallene 5cm brede. Vi kaller det for klassebredden. I dette eksemplet valgte vi klassebredde 5 cm. Dersom vi får en oppgave og klassebredden ikke er gitt er det opp til oss å velge klassebredde slik det er mest hensiktsmessig. Vi setter opp en frekvenstabell: Vi bruker noen parenteser du kanskje ikke har sett før, [ betyr at tallet som kommer
etter skal være med i klassen, mens
I eksempelet over er klassebredden konstant. Slik er det ikke alltid. For litt mer stoff om histogrammer klikk her. Variasjonsbredde = Største verdi - minste verdi I eksemplet over er største verdi 196 cm og minste verdi 150 cm. Variasjonsbredden blir da 46cm. Variasjonsbredden er et mål på spredning. La oss tenke oss at du i løpet av en uke arbeider 7 timer med norsk, 4 timer med engelsk 11 timer med matte og 6 timer med NaMi. Dette kan fremstilles i et sektordiagram på denne måten: Sektordiagrammet viser den innbyrdes fordelingen mellom størrelsene som inngår. For å kunne lage et slikt diagram trenger vi en gradeskive og følgende tabell: I kolonnen til høyre ser du at faktoren 3,6 brukes. Det kommer av at vi tar 360°/100%. Dersom du er interessert i data kan du lage sektordiagrammer og mange andre diagrammer ved hjelp av et regneark program. Figuren er hentet fra et tallbehandlingsprogram som heter Excel og viser noen av de diagramtypene man kan lage med programmet. Ikke overdriv effektene.
|
||||
© 2000- 2024 Sivilingeniør Kenneth Marthinsen, org. no: 976 773 934.
Telefon 932 99 111 Postadr. Odvar Solbergs vei 112, 0973 OSLO
MAIL OSS
|
|
||