|
||||||||||||
 HJEM HJEM |
||||||||||||
| 1. Tall og tallregning | ||||
|
1.1. Innledning | 1.2. Tallsystem | 1.3. Posisjonssystemet | 1.4. Tallinjen | 1.5. Naturlige tall | 1.6. Partall | 1.7. Oddetall | 1.8. Primtall | 1.9. Hele tall | 1.10. Rasjonale tall | 1.11. Reelle tall | 1.12. Fortegn | 1.13. Regnerekkefølge | 1.14. Negative tall | 1.15. Parenteser | 1.16. Huskeregler
Denne siden behandler grunnleggende emner som regnerekkefølge, fortegn, parenteser og litt om tallmengder og tall. Tegnet ≠ brukes, og det betyr "ikke lik".
Vi bruker titallsystemet som består av ti siffer, fra 0 til 9. I tillegg er det slik at plasseringen eller posisjonen til sifferet har betydning for verdien av tallet. Slike systemer kalles posisjonssystemer. Det romerske tallsystemet er et eksempel på at ikke alle tallsystemer er posisjonssystemer. Du kan lese om andre tallsystemer her.
Eksempelvis betyr sifferet 3, i tallet 321, tre hundrere, mens det samme siffer i tallet 13, betyr tre enere. I tallet 0,2, betyr sifferet 2, to tideler, men i tallet 0,002 betyr det samme sifferet to tusendeler. Derfor er det viktig at man plasserer tallene under hverandre når man skal legge sammen og trekke fra.
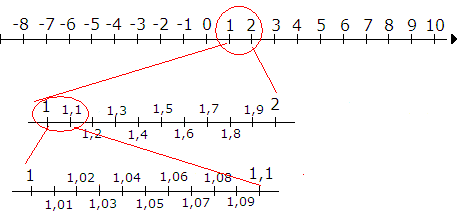
Tallinjen inneholder uendelig mange tall, derfor er det naturlig å dele dem opp i ”familier”. Vi kaller slike familier for tallmengder. Tallene i en tallmengde har gjerne noe til felles.
Figur1.1.: En tallinje inneholder uendelig mange tall.
De naturlige tallene er: 1,2,3,4,5,6,7......... Vi kaller denne tallmengden for N. Partallene er 2,4,6,8,10,12…………. Partall er delelig på to. Partall er en del av de naturlige tallene. Oddetallene er 1,3,5,7,9,11…….. Oddetallene er ikke delelige på to. Oddetall er en del av de naturlige tallene. Dersom du lurer på om et tall kan deles på et annet kan du se på delelighetskriterier. Primtall er naturlige tall som kun er delelige på seg selv og en. Legg merke till at 1 ikke er et primtall. De minste primtallene er: 2,3,5,7,11,13,................... Et naturlig tall som ikke er et primtall kaller vi et sammensatt tall. Sammensatte tall kan faktoriseres. Primtall er en del av de naturlige tallene. Dersom vi tar alle de naturlige tallene inkluderer de hele negative tallene får vi en tallmengde vi kaller for Z, som er de hele tallene. Z : ....., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4,....... En brøk er det vi kaller et rasjonalt tall. Et rasjonalt tall kan skrives som a/b. Alle rasjonale tall har enten en avsluttende desimal (teller delt på nevner har rest null etter et gitt antall desimaler), eller en periodisk desimalutvikling. 1/5 kan skrives som 0,2 2/3 kan skrives som 0,666666666666........... 4/11 kan skrives som 0,363636363636363636........ Det første eksempelet har en avsluttende desimal. Vi ser at i de to siste eksemplene gjentaes sifrene i det uendelige. I tallet 0,666666... kan vi si at perioden er 6. I tallet 0,36363636 er perioden 36. Alle desimaltall som har en periode er rasjonale tall. Vi kaller de rasjonale tallene for Q.
Det finnes enkelte tall som ikke kan skrives som brøk. Et eksempel på det er tallet π (pi). Dersom du prøver å trykke det symbolet på kalkulatoren får du 3,141592654...... Det er ingen periode her, som det er i de rasjonale tallene. Vi kaller denne type tall for et irrasjonalt tall. De rasjonale og de irrasjonale tallene danner den tallmengden som vi kaller for de reelle tallene. Vi bruker symbolet R. R inneholder alle tallene på tallinja.
Figur 1.2.: Figuren viser tallmengdene på tallinja. Legg merke til at N er en delmengde av Z og Z er igjen en delmengde av Q osv.
Et tall kan ha to typer fortegn, negativt eller positivt. Et negativt tall skrives med et minus foran seg. Alle tall som ligger til høyre for null på tallinjen er positive. Alle tall til venstre for null er negative.
Et positivt tall er et tall med positivt fortegn altså et pluss. Vanligvis skriver vi ikke det positive fortegnet. Figur 1.3.: Tallene til høyre for null er positive. Til venstre for null på tallinja er tallene negative. Legg merke til at avstanden fra null til for eksempel 5 og -5 er den samme. Det betyr at tallverdien er lik, men fortegnet er forskjellig. Når vi regner bruker vi forskjellige symboler for de forskjellige regneoperasjoner som addisjon, subtraksjon, multiplikasjon og divisjon. Symbolene er + , - , · og : . På samme måte som andre språk har grammatikk har matematikk også noen regler for hvordan de forskjellige operasjonene skal utføres.
2 + (2 + 13 - 2(1 + 5)) +2= 2 + ( 2 + 13 - 2·6)+ 2 = 2 + 2+ 13 - 12 + 2 = 7
Vi kan overstyre dette ved å bruke parenteser. (5 + 2) · 3 = 7 · 3 = 21 i motsetning til 5 + 2 · 3 = 5 + 6 = 11 Man kan se på hele parentesen som et tall. Addisjon 3 + 2 = 5 3 + 1 = 4 3 + 0 = 3 3 + ( - 1 ) = 2 3 + ( - 2 ) = 1 3 + ( - 3 ) = 0 3 + ( - 4 ) = - 1 3 + ( - 5 ) = - 2 osv. Fra tabellen ser vi at å addere et positivt og et negativt tall er det samme som å trekke fra tilsvarende positivt tall. [ 3 + ( - 2 ) = 1 og 3 - 2 = 1 ]. Subtraksjon 3 - 2 = 1 3 - 1 = 2 3 - 0 = 3 3 - ( - 1 ) = 4 3 - ( - 2 ) = 5 osv. Å subtrahere et negativt tall er det samme som å legge til tilsvarende positive tall. Multiplikasjon Når vi multipliserer et positivt og et negativt tall blir svaret negativt. (-5) · 10 = - 50 Når vi multipliserer to negative tall blir svaret positivt. (-5) · (-10) = 50 Divisjon Når vi dividerer et negativt og et positivt tall blir svaret negativt. 5 : (-10) = - 1/2 Når vi dividerer to negative tall blir svaret positivt. (-5) : (-10) = 1/2
Like tegn blir pluss (++ og --). Ulike tegn blir minus (+- og -+). Når du løser opp en parentes med minus foran, skifter du fortegn på alle tallene inne i parentesen. Dersom du synes dette er vanskelig kan du jo tenke litt på ordenes betydning og så trekke parallellen over til matematikk. " I love you!" + positiv betydning " I do not love you" - negativ betydning " I love you. Not!" + og - gir negativ betydning. " I do not love you. Not!" - og - gir en positiv betydning. (NB: Dette er ikke god engelsk)
|
||||
© 2000- 2024 Sivilingeniør Kenneth Marthinsen, org. no: 976 773 934.
Telefon 932 99 111 Postadr. Odvar Solbergs vei 112, 0973 OSLO
MAIL OSS
|
|
||