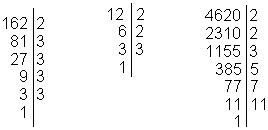Faktorisering | Delelighet | Fellesnevner 

Faktorisering

Faktorisering er ofte brukt i matematikken. Det går ut på å skrive et tall som produktet av faktorer.

Dersom vi skriver 4 som 2 ·2 har vi faktorisert 4. Vi skriver 4 som et produkt av faktorene 2.

Dette bruker vi ofte når vi skal finne fellesnevner eller forkorte.

Dersom vi skriver 8 = 2 · 4 har vi faktorisert 8. Men, vi har ikke primtallsfaktorisert siden 4 ikke er et primtall. Dersom vi skriver 8 = 2 · 2 · 2 har vi primtallsfaktorisert 8.

Gjør følgende:

Skriv tallet som skal faktoriseres på venstre side av en lang loddrett strek. Begynn med å prøve å dele tallet på 2. Dersom det er mulig skriver du 2 på høyre side av streken og svaret du får under tallet på venstre side av streken. Når du ikke kan dele på 2 lenger prøver vi med 3. Slik fortsetter vi med 5, 7 osv. Dersom man multiplisere alle primtallene på høyre side av streken skal man få det tallet man startet med.

16 faktorisert skrives slik:

Vi delte på to fire ganger. Dersom vi multipliserer divisorene ender vi opp med det tallet vi startet med.

Delelighet

Delelig med 2:

Et tall er delelig med to når siste siffer i tallet er delelig med to eller når det slutter på null.

Eksempel 4:

Eks: 24 er delelig med 2 fordi siste siffer, 4, er delelig med 2. 10 er delelig med to fordi det slutter med 0.

Delelig med 3:

Dersom tallets tverrsum er delelig med tre er tallet delelig med tre.

Eksempel 5:

36 er delelig med 3 fordi tverrsummen av 36 er 3 + 6= 9 og 9 er delelig med 3.

Delelig med 5:

Tall som ender på 0 og 5 er delelige med 5.

Eksempel 6:

65 er delelig med 5 fordi det siste siffer i tallet er 5.

Fellesnevner

Når vi skal finne fellesnevner må vi først faktorisere alle nevnerne. Vi bruker metoden over.

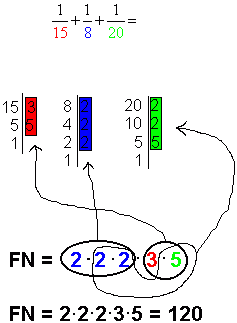
Vi har nevnerne 15, 8 og 20. Disse faktoriseres som vist i eksemplet over. Fellesnevneren må inneholde alle faktorene av 15, 8 og 20.

Vi begynner med den minste faktoren, 2. Den forekommer tre ganger i 8 og to ganger i 20. Vi har følgende regel:

"den som har flest vinner".

Det betyr at vi trenger tre 2 -ere i fellesnevner. Neste tall er 3, som det bare er en av. Vi ser at det er to 5 -ere, en fra 15 og en fra 20. Vi tar med en 5 -er.

Fellesnevner, som også kalles minste felles multiplum, er:

FN = 2 · 2 · 2 · 3 · 5 = 120

Figuren viser at fellesnevner inkluderer alle faktorene som forekommer i hver av de faktoriserte nevnerne.

De faktorene som er med i fellesnevner og ikke i brøkens nevner, er de faktorene brøken må utvides med for at man oppnår å få fellesnevner i brøken. (se siden som omhandler brøk).