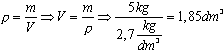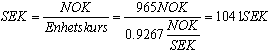|
||||||||||||
 HJEM HJEM |
||||||||||||
| Matematikk i Dagliglivet | ||||
|
Tid | Vei Fart og Tid | Massetetthet | Valuta | Målestokk Vi måler tid i sekunder, minutter og timer. En time består av 60 minutter og et minutt av 60 sekunder. Basisen er i dette systemet er 60 og stammer fra babylonsk matematikk. Fra desimalsystemet er vi vant med del av 10, eller del av 100. Minutter og sekunder er del av 60. Dette skaper ofte noe forvirring. La oss se på to eksempler:
Eksempel 1:
Hvor mange minutter er 0,75 timer? Vi vet at en time består av 60 minutter.
Eksempel 2:
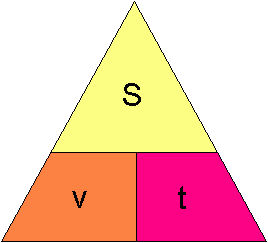
Hva er 75 minutter omgjort til desimal tid? 75 minutter : 60 = 1,25 time For å huske om vi skal gange eller dele kan vi sette opp følgende trekant:
Trekanten brukes på følgende måte: Hold fingren over det du ønsker å finne. Dersom det du ser når du gjør det står ved siden av hverandre multipliserer du. Dersom de to kjente størrelsene står over hverandre dividerer du den øverste på den nederste. Denne metoden bruker du på alle andre trekantfigurer på denne siden.
Eksempel 3:
Hva er den naturlige måten å uttrykke 2,57 timer på? Vi har 2 hele timer + 0,57 · 60 minutter = 2 timer og 34,2 minutter. Vi har følgende sammenheng mellom vei, fart og tid v - fart, kommer fra det engelske ordet velocity. t - tid. s - strekning. Fart har benevningen meter per sekund (m/s) eller kilometer per time (km/t). Dersom du ferdes på sjøen eller i luften måles gjerne farten i knop. En knop er 1852m/time. Følgende figur kan hjelpe deg å huske formelen:
Trekanten brukes på samme måte som den over. Dersom du skal finne s holder du fingren over s og ser da at v og t står ved siden av hverandre. Du ganger v og t. Skal du finne t tar du s delt på v.
Eksempel 4:
En bil kjører 50 km på 45 minutter. Hva er bilens gjennomsnittsfart? Det kan tenkes at du har behov for å regne om fra m/s til km/t. Det er 3600 sekunder i en time (60 · 60). Dersom du har en fart oppgitt i meter per sekund ganger du med 3600. Det tallet du da får er meter per time. Det er 1000m i en kilometer. Det betyr at du må dele det tallet du har på 1000. Er du lur, slår du begge operasjonene sammen og ganger med faktoren 3,6. Når du går fra km/t til m/s deler du tallet i km/t på 3,6, av samme grunn som over. Regel: Fra km/t til m/s: del på 3,6 Fra m/s til km/t: gang med 3,6 Vi bruker symbolet
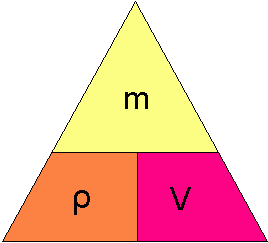
Massetetthet er lik masse delt på volum.
Vann har massetetthet 1. Alt som har massetetthet mindre enn 1 flyter. Alt som har massetetthet større enn 1 synker. Massetettheten har benevning g/cm3 eller kg/dm3.
Eksempel 5:
Massetettheten av et stoff er:
Pilene du ser her kalles implikasjon og kan leses som ”fører til”. Merk at benevningen ”faller” direkte ut av regnestykket fordi vi satte inn den som var mest hensiktsmessig i forhold til kilo. Vi kunne ha brukt g/cm3, men da måtte vi ha regnet om 5 kilo til gram.
Eksempel 6:
Hva er massetettheten av et stoff når volumet er 47cm3 og massen er 1 kg? Finnes det noen stoffer som har en så høy massetetthet? Vi bruker penger som byttemiddel.
I Norge kaller vi disse pengene for kroner, forkortet NOK. Disse har samme verdi
i hele landet. Disse forskjellige byttemiddlende kaller vi for valuta. Forskjellig valuta har forskjellig verdi. Vi kan kjøpe utenlandsk valuta fra bankene. Prisen på valutaen kalles for kurs. Kurs oppgies for 100 enheter av fremmed valuta. Det finnes tre unntak; Euro (€), GBP (£ britiske pund) og USD ( $ amerikanske dollar). Kursen for disse oppgies for en enhet. Bankene har to kurser, en for kjøp og en for salg. (Husk at det er sett fra bankens side, når du kjøper selger banken.) Kursen for salg er høyere enn kursen for kjøp. Det betyr at dersom du har penger til overs fra utenlandsferien og vil veksle tilbake til NOK taper du penger dersom kursen er uforandret. Enhetskurs Prisen vi må betale for en valutaenhet: NB! Dette gjelder ikke Euro, britiske pund (£) og amerikanske dollar ($). Disse er oppgitt i enhetskurs så du skal ikke dele på 100. Følgende sammenheng gjelder: Dette kan illustreres med en trekant:
Gebyr Du må vanligvis betale noe for at bankene skal selge deg noe (ganske utrolig egentlig). Det kalles for et gebyr. Dersom du skal kjøpe GBP (britiske pund) for 1000 kr og banken tar et gebyr på kr. 50 betyr det at du bare har 950 kr å kjøpe GBP for. Trekk alltid fra gebyret før du begynner valuta omregningen. Vi regner fra norske kroner til utenlandsk valuta:
Eksempel 7:
Vi skal kjøpe svenske kroner for 1000 norske kroner. Kursen er 92,67. Gebyret er 35kr. Hvor mange svenske kroner får vi? Vi trekker først fra gebyret. Vi har da 965 NOK å kjøpe SEK for. Vi får: Vi får 1041 svenske kroner for 965 norske når kursen er 92,67. Vi regner fra utenlandsk valuta til norske kroner:
Eksempel 8:
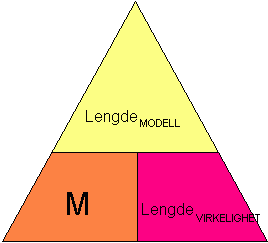
Et stereoanlegg koster 5525 DKK (danske kroner), kursen er 121,12. Hva koster stereoanlegget i norske kroner? NOK = 5525 DKK · 1,2112 NOK/DKK = 6692 NOK Her kan du finne valutakurser fra Norges bank. La oss kalle målestokken for M. Vi har følgende formel: LengdeMODELL kan være lengden på et kart, lengden av et fly, en båt, osv. Dersom LengdeMODELL er lengden på et kart vil Lengde VIRKELIGHET være lengden i landskapet.
Lengde VIRKELIGHET og Lengde MODELL har ALLTID samme benevning.
M har ikke noen benevning, men er et forhold mellom to lengder med samme benevning. Dersom M er mindre enn en (M<1) har vi en forminskning. Det betyr at modellen vår er mindre enn det som er virkeligheten. Dersom M er større enn en (M>1) har vi en forstørring. Det betyr at modellen vår er større enn det som er den virkelige tingens størrelse. M kan skrives på tre måter: Alle tre måtene er likeverdige, men den første måten er vanligst. Dersom du har bygget modellfly eller båter har du sikkert lagt merke til at det står noen tall utenpå esken. Det kan være 1:20, 1:50, 1: 100 osv. Det er målestokken. Om målestokken er 1:20 betyr det at 1 lengdeenhet på vår modell er 20 lengdeenheter i virkeligheten. Vi leser 1:20 som "en til tjue". Vi har laget en "husketrekant" som brukes som alle andre trekanter på denne siden.
Eksempel 9:
Et kart har målestokk 1: 25000. Dersom du måler 4cm på kartet hvor langt er det i terrenget? Vi kjenner M og vi kjenner LengdeMODELL. Det vi skal finne er LengdeVIRKELIGHET. Regnestykket vårt blir:
LengdeVIRKELIGHET =
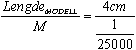 =
4 cm ⋅ 25000 = 1000000 cm = 1 km =
4 cm ⋅ 25000 = 1000000 cm = 1 km
Eksempel 10:
En modell av en båt er i målestokk 1:100. I virkeligheten er båten 72 meter lang. Hvor lang er modellen?
LengdeMODELL = LengdeVIRKELIGHET ⋅ M = 72 m ⋅
Eksempel 11:
Et smykke er 12mm bredt. For å vise detaljene i smykket har kunstneren laget en modell som er 36cm bred. Hva er målestokken? Dette er et spesielt tilfelle siden modellen er større enn virkeligheten. Normalt er det motsatt.
|
||||
© 2000- 2024 Sivilingeniør Kenneth Marthinsen, org. no: 976 773 934.
Telefon 932 99 111 Postadr. Odvar Solbergs vei 112, 0973 OSLO
MAIL OSS
|
|
||