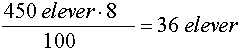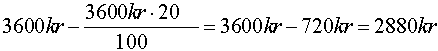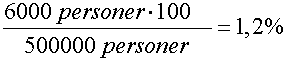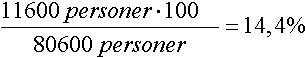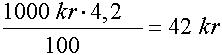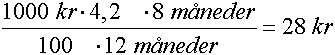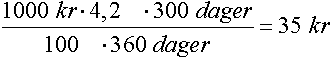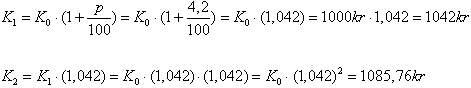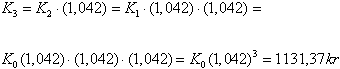|
||||||||||||
 HJEM HJEM |
||||||||||||
| Prosent | ||||
|
Grunnlag | Endringer | Banksparing | Prosentvis & eksponentiell vekst Med prosent mener vi "del av hundre". Vi bruker tegnet %.
Eksempel 1:
58% er det samme som Som du ser er det en sammenheng mellom prosent, brøk og desimaltall. Desimaltallet, i dette tilfellet 0,58, kalles ofte prosentfaktoren. Skal vi gå fra prosent til brøk tar vi prosenten og deler på 100. Utfører vi divisjonen finner vi prosentfaktoren: Vi har følgende ligning som kan gi svar på det meste av det som kan spørres om angående prosent:
(1)
Eksempel 2:
På en skole med 450 elever svarte 8% at de ble mobbet på skolen. Hvor mange elever ble mobbet? Vi bruker (1) og får:
Eksempel 3:
En TV er på tilbud. Full pris er 3600 kr. Hva koster den når man får 20% rabatt? Vi bruker ligning (1) her også, men legg merke til at det spørres etter differansen mellom fullpris og 20%. Derfor tar vi hele summen før avslag og trekker fra de tjue prosentene som utgjør avslaget. Dersom vi skal finne prosenten bruker vi fortsatt ligning (1), men vi omformer den slik at vi får:
(2) Prosenten:
Eksempel 4:
Av en befolkning på 500.000 er det 6000 som lider av schizofreni. Hvor mange prosent lider av sykdommen? Vi bruker (2) og får: Hele tallet kan man finne når prosenten og delen av tallet er kjent. Vi bruker:
(3)
Eksempel 5:
På en arbeidsplass var det 8 personer som var syke. Det var 20% av alle ansatte. Hvor mange ansatte var det på arbeidsplassen? Vi bruker (3) og får Altså var det 40 personer som var ansatt på dette stedet. Det spørres ofte etter endringer. Husk på at endringen kan betraktes som del av tallet. Hele tallet blir da tallet før endringen.
Eksempel 6:
Prisen på en bolig steg fra kr. 1.600.000 til kr. 1.900.000 på et år. Hva var prisstigningen i prosent? Endringen: 1.900.000kr. - 1.600.000 = 300.000 kr. Her er hele tallet 1.600.000 da dette var verdien på boligen før endringen. Vi bruker (2) og får:
Eksempel 7:
Antall arbeidsledige går ned fra 80600 til 69000, fra en måned til den neste. Hvor stor var nedgangen i prosent? Vi får: 80600 personer - 69000 personer = 11600 personer Innsatt i (2) får vi: Banken betaler deg penger for at den får lov til å disponere sparepengene dine. Det kalles renter. Hvor mange kroner du får i renter kommer an på prosenten, eller rentefoten og hvor mye du sparer. Dersom banken tilbyr 4,2% renter p.a. (per år) og vi sparer 1000 kr. i et år, bruker vi formel (1).
Eksempel 8:
Det er tolv måneder i et år. Dersom du sparer i åtte måneder, med betingelsene fra forrige eksempel får vi:
Eksempel 9:
Bankene regner at et år har 360 dager. Dersom du sparer 1000 kr i 300 dager med 4,2% rente får vi:
Eksempel 10:
Prosentvis & eksponentiell vekst La oss tenke oss at vi sparer kr. 1000,- og at rentefoten er 4,2%. Hvor mye har vi på konto etter 8 år? Vi må da ta hensyn til rentene vi tjener det første året. Det beløpet blir lagt til de 1000 kronene og er en del av grunnlaget for rentene det andre året. Slik fortsetter det hvert år. La oss bruke formel (1) og se: År 1: Det første året tjente vi kr 42 i renter. Dette legges til det beløpet vi startet med, slik at ved inngangen til det andre året er sparebeløpet vårt kr 1042. År 2: Ved starten av det tredje året vil sparebeløpet vårt være 1042 kr + 43,76 kr = 1085,76 kr. Slik kan vi fortsette til vi har resultatet for det 8. året. Når vi regner renter av rente kaller vi det for rentersrente. Vi skal nå finne en enklere måte å beregne rentersrente på. La oss kalle de 1000 kronene vi begynner med for K0. La oss kalle sparebeløpet ved første årsskifte for K1. La oss kalle rentefoten for p. Vi har da følgende situasjon. K2 er pengene vi har i banken etter to år. Fra slutten av første til slutten av andre året vokser pengene med en faktor 1,042. Slik fortsetter det. Etter tredje året har vi K3: 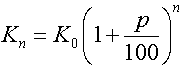 Dette er formelen for prosentvis vekst, også kalt eksponentiell vekst. K0 er det vi har til å begynne med Kn er det vi har etter n år, n er antall år og p er prosenten det vokser med. Anvender vi denne formelen på problemet vårt finner vi at beløpet vårt etter åtte år er: |
||||
© 2000- 2024 Sivilingeniør Kenneth Marthinsen, org. no: 976 773 934.
Telefon 932 99 111 Postadr. Odvar Solbergs vei 112, 0973 OSLO
MAIL OSS
|
|
||