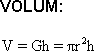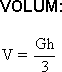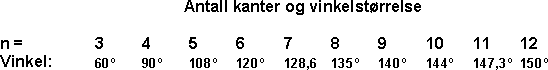|
||||||||||||
 HJEM HJEM |
||||||||||||
| Geometri III | ||||
|
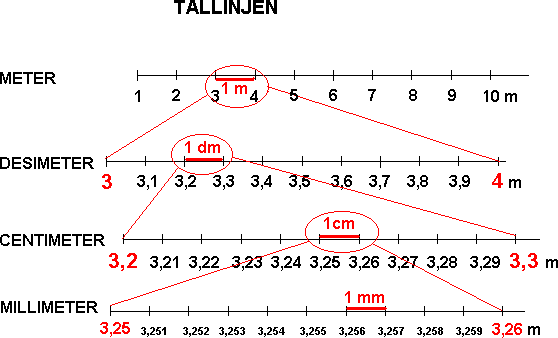
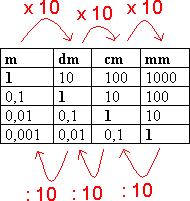
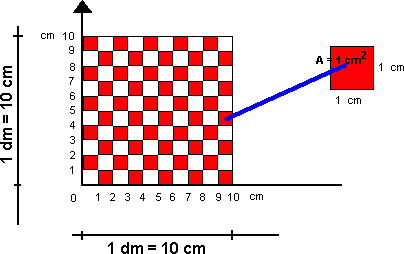
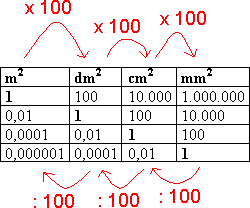
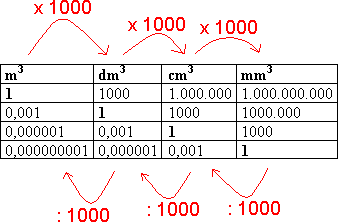
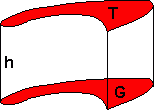
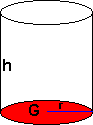
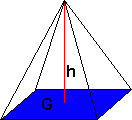
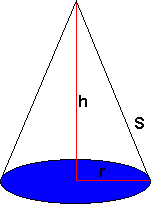
Omregningstabeller | Kongruente Former | Volum og Overflate | Formlikhet | Mangekanter | Tesselering (Flislegging) | Fibonacci | Det Gylne Snitt | Fraktaler | Spiraler Lengde En lengde er gitt ved et måltall og en enhet. Enheten kalles for benevning. Eksempler på enheter er meter (m), desimeter (dm), centimeter (cm) og millimeter (mm). Vi har følgende sammenheng: 1m = 10dm = 100cm = 1000mm Skal man arbeide med flere lengder er det viktig at alle har samme enhet. Vi går fra en enhet til en mindre enhet ved å multiplisere måltallet med 10. Motsatt vei dividerer vi med 10. Ønsker man for eksempel å gå fra meter til centimeter må man multiplisere med 10 to ganger. For større lengder har vi enhetene kilometer (km) og mil. 1km = 1000m = 0,1mil. 1 mil = 10km Areal Et areal er gitt ved et måltall og en enhet. Enheten kalles for benevning. Eksempler på enheter er kvadratmeter (m2), kvadratdesimeter (dm2), kvadratcentimeter (cm2) og kvadratmillimeter (mm2). Vi har følgende sammenheng: 1m2 = 100dm2 = 10000cm2 = 1000000mm2 Skal man arbeide med flere areal er det viktig at alle har samme enhet. Vi går fra en enhet til en mindre enhet ved å multiplisere måltallet med 100. Motsatt vei dividerer vi med 100. Ønsker man for eksempel å gå fra kvadratmeter til kvadratcentimeter må man multiplisere med 100 to ganger. Volum Et volum er gitt ved et måltall og en enhet. Enheten kalles for benevning. Eksempler på enheter er kubikkmeter (m3), kubikkdesimeter (dm3), kubikkcentimeter (cm3) og kubikkmillimeter (mm3). Vi har følgende sammenheng: 1m3 = 1000dm3 = 1000000cm3 = 1000000000mm3 Skal man arbeide med flere volum er det viktig at alle har samme enhet. Vi går fra en enhet til en mindre enhet ved å multiplisere måltallet med 1000. Motsatt vei dividerer vi med 1000. Ønsker man for eksempel å gå fra kubikkmeter til kubikkcentimeter må man multiplisere med 1000 to ganger. Når man regner ut et volum regner vi med en eller flere lengder. Når det arbeides med flere lengder må alle ha samme enhet. Se avsittet foran, om lengder. For større arealer har vi følgende enheter: ar = 100 m2, daa = dekar = 1 000 m2, ha = hektar = 10 000 m2, km2 = kvadratkilometer = 1 000 000 m2. Geometriske figurer som dekker hverandre helt når vi legger den oppå hverandre kalles for kongruente. Det kan tenkes at vi må rotere figurene for at de skal dekke hverandre. Dersom figur B roteres 90º med klokka, ser vi at figur A og B dekker hverandre helt. A og B er kongruente figurer. Dersom grunnflaten G og toppflaten T er to parallelle, kongruente plan er volumet gitt ved:
V = Grunnflate · høyde = G · h
Legemets overflate er gitt ved:
O = 2 · Grunnflate + OmkretsGrunnflate · høyde = 2G + OGh
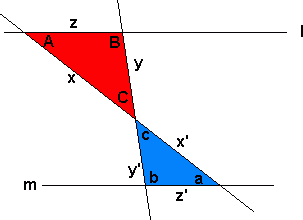
Sylinder Pyramide Kjegle Kule En trekant er formlik med en annen trekant dersom vinklene i begge trekantene er like store. Dersom vi skal påvise at to trekanter er formlike må vi vise at to av vinklene i trekantene er identiske (den tredje gir seg da selv). I denne figuren er rød trekant formlik blå trekant fordi linjene l og m er parallelle og fordi vinkel C og c er toppvinkler. Vinkel A = a, B = b og C =c. Vi har følgende forhold mellom lengdene på sidekantene i trekantene: Uttrykkene over kalles for proporsjoner og utrykker følgende på norsk: Forholdet mellom to sider i den ene trekanten er lik forholdet mellom tilsvarende sider i den andre trekanten. Dette gjelder bare når trekantene er formlike. En mangekant er en geometrisk figur med tre eller flere kanter. Alle mangekanter kan deles inn i trekanter. Alle trekanter har en vinkelsum på 180º En figur med n kanter kan deles opp i (n-2) trekanter. Vinkelsummen av n - kanten blir (n-2)180º.
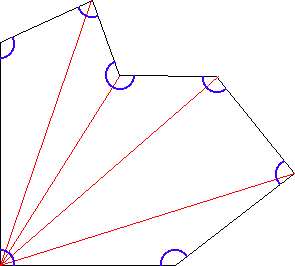
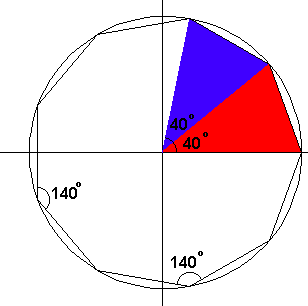
Regulære mangekanter En regulær mangekant er en geometrisk figur der alle sider er like lange og alle vinkler er like. I en regulær n - kant er vinkelen Alle regulære mangekanter kan innskrives i en sirkel, som vist under. Tilsvarende sier vi at sirkelen er omskrevet en mangekant. Tegning av Regulære Mangekant Vi kan tegne regulære mangekanter på følgende måte: Slå en sirkel. Avsett et tilfeldig punkt på sirkelbuen. Dersom du skal tegne en n-kant deler du gradeantallet i sirkelen (360º) på n. La oss tegne en 9 kant. Da får vi 360º : 9 = 40º. Vi bruker transportøren (gradeskiven) og deler sirkelperiferien opp i 40 graders sektorer. Tegningen kan se slik ut: Legg merke til at mangekantens vinkel øker sterkt når n er liten, men avtar med voksende n. Når n blir stor går mangekanten mot en sirkel. Å dekke en flate med fliser kalles tesselering. Til dette kan man bruke flis med varierende størrelse og form. Dersom man ønsker å bruke regulære mangekanter må man være oppmerksom på følgende: Der to eller flere mangekanter møtes blir vinkelsummen 360º. Det betyr at den regulære mangekantens vinkel må innfri følgende krav:
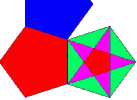
Mangekantens vinkel · Antall flis som møtes =360º
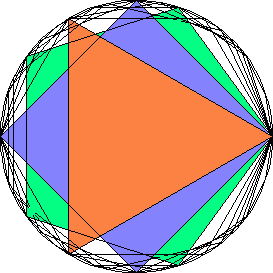
Dersom ikke dette er oppfylt vil ikke flisene dekke hele flaten. Det vil bli en glipe i punktet der flere flis møtes. Fra tabellen avsnittet om mangekanter ser vi at det kun er regulære tre-, fire- og sekskanter som oppfyller dette kravet. Figuren viser tesselering med forskjellige typer regulære mangekanter. Vi ser at med regulære femkanter blir det umulig å dekke flaten. Man kan selvfølgelig benytte forskjellige regulære mangekanter til tesseleringen. Vi har tallfølgen:
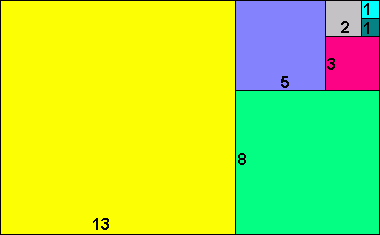
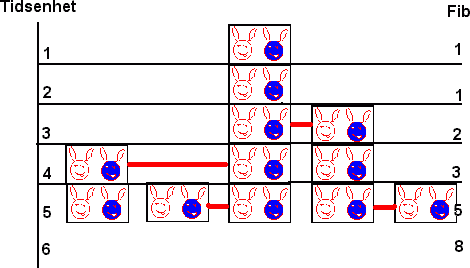
1, 1, 2, 3, 5, 8, 13, 21, 34,........
Tallene kalles for Fibonaccitallene og fremkommer ved at et tall i følgen er summen av de to foregående. F(n) = F(n-1) + F(n-2) n > 2 Disse tallene finner du igjen i naturen, i mange sammenhenger. Dersom man ønsker et grafisk bilde av tallene kan man tenke seg at tallene beskriver sidene i et kvadrat. Når man legger kvadratene ved siden av hverandre kan man oppnå følgende mønster: Fibonacci var en Italiensk matematiker som levde mellom 1170 og 1250. De påståes at han kom fram til disse tallene ved å studere kaniner. Tenk deg følgende:
Hva synes du om denne modellen? Dersom vi følger modellen, hvor mange kaniner er det på øya et år senere? Figuren under setter deg på sporet.. Det gylne snitt er en måte å dele linjer på. Dette forekommer når forholdet mellom linjestykkene er som følger:
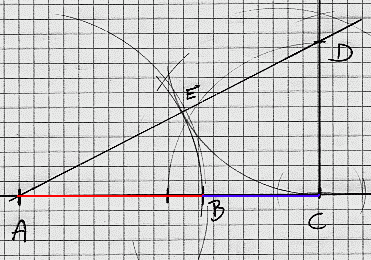
Dersom b deler linjestykket AC i et gyllent snitt har vi følgende: AC = 1,618AB AB = 0,618AC Vi finner det gylne snitt ved konstruksjon på følgende måte:
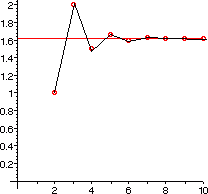
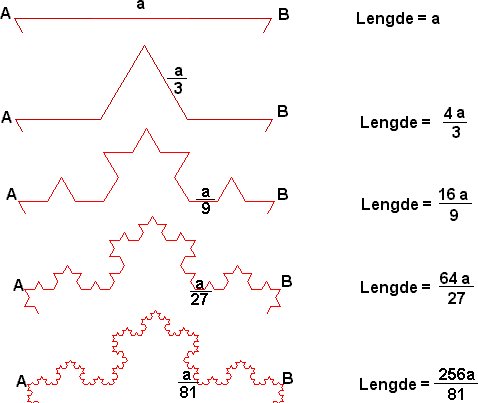
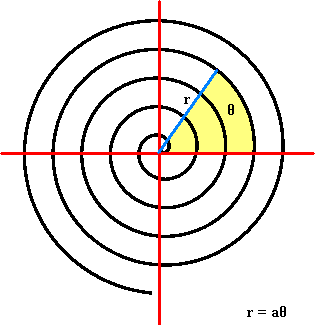
Det gylne snitt spiller en sentral rolle i fotografi og annen billedkunst. Dersom vi benytter det ovenstående på sidene i et fotografi får vi følgende: Som du ser kan det gylne snitt også anvendes på flate. En gyllen trekant er en likebeint trekant der forholdet mellom langside og kortside er 1,618. Du har tidligere stiftet bekjentskap med Fibonaccitallene. Dersom vi tar Fib(2):Fib(1), Fib(3):Fib(2), Fib(4):Fib(3)...osv. Finner vi følgende: Plotter vi grafen ser det slik ut: Tenk på strømningene i en stri bekk, skyene på himmelen og sanddyner som formes. Alle disse systemene er i stadig endring og kan se ut som det reneste kaos. Fraktalgeometrien ble utviklet for å analysere og beskrive slike kaotiske systemer. En fraktal er en kurve, figur eller gjenstand som er formlik med seg selv. Deler av fraktalen har samme form som hele fraktalen. Man kan tenke seg en fraktal som en uendelig lang linje på et endelig areal. La oss se: Utviklingen av datateknologi og regnekraft må ta mye av æren for fraktalenes popularitet. I tillegg til at de kan hjelpe oss til å forstå kompliserte problemer er de jo ganske pene å se på også. Nedenfor ser du eksempler på fraktaler. Dersom du har mobiltelefon er det svært sannsynlig at antennen i telefonen har en fraktalgeometri. En spiral er en kurve som beskrives av et punkt som roterer rundt en pol, et fast punkt, som det roterende punkt fjerner seg fra. Det finnes mange varianter av både krumme og brukkne spiraler. To krumme er disse: Arkimedes' Spiral Tenk deg en stor klokke som har en to meter lang "langeviser" (den som bruker en time på en runde.)Tenk deg vider at en flue sitter i sentrum av klokken, men på denne viser. Fluen begynner å gå mot tuppen av viseren med en konstant fart på 0,5 meter per time. Bevegelsesmønsteret til fluen er beskrevet ved denne type spiral. Avstanden mellom hvert omløp er det samme. Ligningen i polare koordinater er r=aθ der r er radien, a er en konstant og θ er vinkelen. Logaritmisk Spiral En logaritmisk eller likevinklet spiral er formlik med seg selv og alle andre likevinklede spiraler. Det betyr at spiraler av denne typen er sammenfallende dersom man forstørrer/ forminsker. Spiralens avstand til "seg selv" øker for hvert omløp. Vinkelen θ, mellom en linje OP og spiralen, er fast.
|
||||
© 2000- 2024 Sivilingeniør Kenneth Marthinsen, org. no: 976 773 934.
Telefon 932 99 111 Postadr. Odvar Solbergs vei 112, 0973 OSLO
MAIL OSS
|
|
||