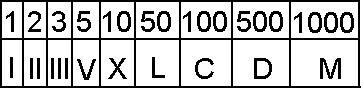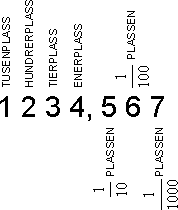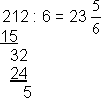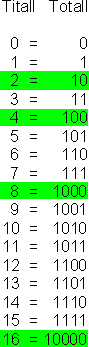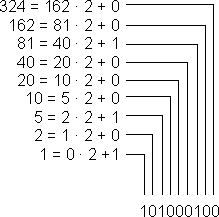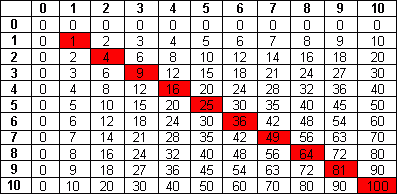
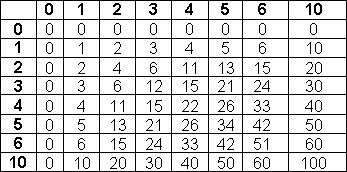
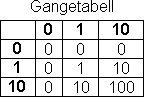
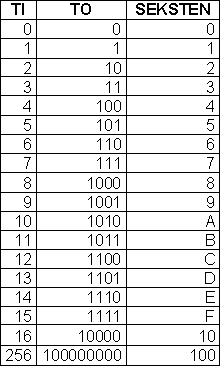
Romertall | Titallsystemet | Syvtallsystemet | Totallsystemet | Det Heksadesimale Tallsystem 

Romertall

I liket med andre kulturer benyttet romerne bokstaver for å symbolisere tall.

For å unngå mer enn tre like tegn ved siden av hverandre skrives for eksempel 4 som IV. Regelen er at når en bokstav med lavere verdi kommer foran en med større verdi, trekkes den laveste verdien fra den største (4 = 5 - 1). Systemet er lite praktisk å regne med.

Titallsystemet

Vi benytter til daglig et tallsystem vi kaller Titallsystemet. Titallsystemet benytter ti siffer, fra 0 til 9. Titallsystemet er et posisjonssystem. Det betyr at et siffer betydning, er avhengig av posisjon. Her er noen posisjoner:

Tallverdien er avhengig av sifferets verdi og posisjon.

Titallsystemet, gangetabell.

Syvtallsystemet

La oss bruke syv som grunntall i stede for ti. Syvtallsystemet er lite anvendt, utover mulig pedagogisk trening. For å skille de forskjellige tallene i de forskjellige tallsystemene fra hverandre bruker vi indekser. 100_syv= ( 1·7² +0·7¹+0·7⁰)_ti= 49_ti. På den annen side er 100_ti=( 2·7² +0·7¹+2·7⁰)_ti= 202_syv. Dette viser at forestillingen om "runde tall", er avhengig av tallsystem. Multiplikasjonstabellen ser slik ut:

Desimaltall
EKS:
(56,23)_syv = ( 5·7¹ + 6·7⁰+ 2·7^-1 + 3·7^-2)_ti = ( 35 + 6 + 2/7 + 3/49)_ti ≈ 41,347_ti

Divisjon
EKS:

Totallsystemet

Totallsystemet brukes mye i forbindelse med datamaskiner. Systemet består av sifrene 0 og 1, det medfører at tallene har en tendens til å bli lange og plasskrevende. Totall systemet er, i likhet med titallsystemet et posisjonssystem. Her er noen av tallene:

Regneregler:

La oss sjekke multiplikasjonen ved å gjøre om til titallsystemet. Dette er potensregning.

11101_to= ( 1· 2⁴ + 1 · 2³ + 1 · 2² + 0 · 2¹ + 1 · 2⁰ )_ti= (16 + 8 + 4 + 0 + 1)_ti = 29_ti.

10000001_to = ( 1· 2⁷ + 0 · 2⁶ + 0 · 2⁵ + 0 · 2⁴ + 0 · 2³ + 0 · 2² + 0 · 2¹ + 1 · 2⁰)_ti = (128 + 1)_ti=129_ti.

111010011101_to =
( 1 · 2¹¹ + 1 · 2¹⁰ + 1 · 2⁹ + 0 · 2⁸ 1· 2⁷ + 0 · 2⁶ + 0 · 2⁵ + 1 · 2⁴ + 1 · 2³ + 1 · 2² + 0 · 2¹ + 1 · 2⁰)_ti =
(2048 + 1024 + 512 + 0 + 128 + 0 + 0 + 16 + 8 + 4 + 0 + 1)_ti = 3741_ti

I titallsystemet kan vi kontrollere: 29 · 129 = 3741

Vi har sett hvordan vi regner om fra totall- til titallsystemet. Når skal vi gå motsatt vei. Vi skal gjøre 324_ti om til titallsystemet. Måten det gjøres på er at man dele på to (heltallsdivisjon) og beholder resten. Når vi deler på to kan resten bli en eller null. Vi bygger opp tallet i totallsystemet bakfra, som vist under.

Som vi ser er 324_ti=101000100_to. Synes du totallsystemet blir for plasskrevende kan du jo sjekke ut det heksadesimale (16) tallsystemet.

Det Heksadesimale Tallsystem

Tallsystemet brukes mye innen it- faget. Her er noen av tallene:

EKS: A0F_seksten= (10 · 16² + 0 · 16¹ + 15 · 16⁰) _ti = (2560 + 0 + 15)_ti = 2575_ti