7.1 Funksjonsbegrepet
Regel:
y er en funksjon av x dersom hver mulig verdi for x gir nøyaktig én verdi for y.
7.2 Grafen til en funksjon
Når vi skal tegne grafen til en funksjon f, velger vi noen verdier for x og regner ut funksjonsverdiene f(x). Disse punktene plotter vi i et koordinatsystem og trekker en kurve gjennom de. Vi ser her på funksjonen f med funksjonsuttrykket
Det gir denne funksjonstabellen (utregningene er ikke tatt med):
| x | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) | 8 | 3 | 0 | -1 | 0 | 3 | 8 |
Vi markerer punktene (x, f(x)) i et koordinatsystem og får denne grafen:
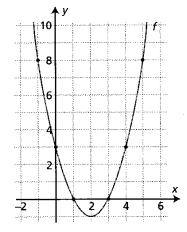
Vi kan også få opp funksjonsverdiene på lommeregneren ved å gå inn på TABLE. Her skriver vi inn funksjonen, velger F5 (RANG) og setter inn verdier som passer til grafen. I tilfellet overfor vil det være:
TABLE RANGE
Start: -1
End: 5
Pitch: 1
7.3 Nullpunkt, toppunkt og bunnpunkt
I 7.2 tegnet vi denne grafen:
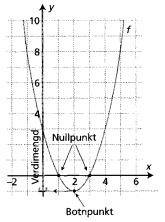
Regel:
x er et nullpunkt for f hvis f(x) = 0
De x-verdiene der f(x) = 0 kaller vi nullpunktene til f. På grafen finner vi nullpunktene der grafen skjærer x-aksen. Denne funksjonen har nullpunktene x = 1 og x = 3.
Vi har også et bunnpunkt i punktet (2, -1). I et bunnpunkt er funksjonsverdien mindre enn alle nabopunktene. En funksjon kan også ha et toppunkt. Det er et et punkt der funksjonsverdien er større enn alle nabopunktene.
Noen funksjoner har både bunnpunkt og toppunkt. Dette er grafen til funksjonen
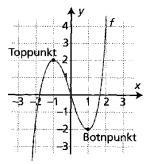
Grafen har et toppunkt i (-1, 2) og et bunnpunkt i (1, -2). Disse punktene er imidlertid bare lokale topper og bunner, da de ikke er funksjonenes høyeste og laveste verdier.
For å finne toppunktene og bunnpunktene på lommeregneren velger vi GRAPH på ikonmenyen og legge inn funksjonsuttrykket:
Y1 = -X2 + 2X + 3
Vi velger G-Solv, og så F1 (ROOT). Vi finner da nullpunktene, som er x = -1 og x = 3.
Toppunkt: G-Solv, F2 (MAX), (1, 4)
Bunnpunkt (ikke på denne grafen): G-Solv, F3 (MIN).
7.4 Grafiske løsninger
Etter å ha tegnet opp en funksjon, leser vi at dataene på denne måten:
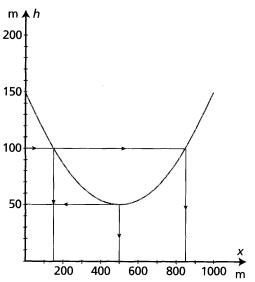
7.5 Andregradsligninger med to ledd
Ligningen
kaller vi en andregradsligning. Vi løser den på denne måten:
x2 = 4
x = 2 eller x = -2
Vi skriver ofte bare x = ±2 isteden for ovennevnte.
Regel:
Hvis konstantleddet c mangler får vi en andregradsligning av denne typen:
Når vi multipliserer to tall som ikke er null, kan vi ikke få null som svar. Hvis vi vet at produktet av to tall er null, så må altså et av tallene være null. Denne slutningen kaller vi produktregelen:
Produktregelen:
7.6 Andregradsformelen
Regel:
Andregradsligningen ax2 +bx +c har løsningene:

når b2 - 4ac ≥ 0.
7.7 Praktisk bruk av andregradsligninger
Siden dette er en regelbok, tar jeg ikke med eksemplene som er vist i boka. Du må som kjent kunne stoffet for å nyttegjøre deg av regelboka, og jeg tar her bare for meg grove trekk i lærebokstoffet.
7.8 Polynomfunksjoner
Uttrykkene 2x + 3 og x2 + 3x - 5 kaller vi polynom. Uttrykket 2x + 3 er et polynom av første grad, og uttrykket x2 + 3x - 5 er et polynom av andre grad.
Den høyeste eksponenten til variabelen i et polynom kaller vi graden til polynomet. Polynomet 2x3 + 3x2 - 6x + 4 er av tredje grad, og polynomet x4 + 2x2 + 5x + 4 er av fjerde grad.
7.9 Rasjonale funksjoner
Regel:
En rasjonal funksjon har et bruddpunkt der nevneren er null.