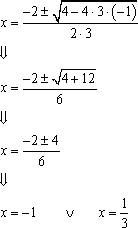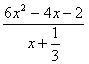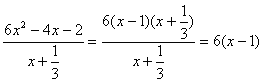Andregradsligninger på standardform | Andregradsligninger på produktform | Faktorisering av andregradsuttrykk | Sum og produkt av røtter 

Andregradsligninger på standardform

Vi forutsetter at du kan stoffet i ligninger , ligninger med to ukjente og funksjoner I og II.

Fra siden om potenser vet vi at x x = x². Sagt med ord sier vi at "x multiplisert med seg selv er lik x i andre". Andregradsligninger inneholder alltid et ledd hvor x² er en faktor. Vi ønsker alltid å få ligningen på formen:

Dersom noen av leddene er på høyre side av likhetstegnet flyttes de over på venstre side, med motsatt fortegn, slik at vi får ligningen på formen i (1). a, b og c er konstanter. Dersom a = 0 har vi en vanlig ligning som løses med metoden beskrevet i ligninger. Dersom b = 0 har vi følgende formel:

Dersom c = 0 har vi følgende formel:

Alle disse tre varianter av mulige andregradsligninger kan løses ved hjelp av formelen:

Tegnet leses "pluss eller minus".

Alle tre eksemplene har gitt løsninger av ligningene. Det er mange ligninger som ikke har løsninger. La oss knytte eksemplene opp mot funksjoner og se litt nærmere på dem.

La oss tenke oss at vi har funksjonen:

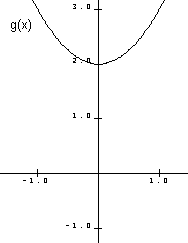
Dersom vi setter f(x) = 0 får vi andregradsligningen i eksempel en. La oss se på grafen til f(x):

Man ser at løsningen på andregradsligningen i eksempel en stemmer over ens med punktene der grafen til f(x) krysser x- aksen, altså der f(x) = 0.

La oss se på funksjonen g(x) = x²+ 2

Som du ser krysser aldri grafen til g(x) x-aksen. Dersom du prøver å løse ligningen g(x) = 0 vil du finne ut at du får et negativt tall under rottegnet. Ligningen har ingen løsninger.

Du lurer kanskje på hvor formel (4) kommer fra. Nedenfor følger en utledning fra andregradsligningen til formelen. Det sentrale punkt i utledningen er manipuleringen for å få første kvadratsetning.

Vi kjenner nå andregradsligninger på formen

ax² + bx + c = 0

Vi vet at den lar seg løse (viss den har løsninger) ved å sett a, b og c inn i

Andregradsligninger på produktform

Man kan ha andregradsligninger på formen:

(x + 1)(x – 2) = 0

{ Du ser at dette er en andregradsligning om du multiplisere ut parentesene:

(x + 1)(x – 2) = x² -2x +x – 2 = x² – x – 2  }

Man kan multiplisere ut faktorene som vist over og bruke abc – formelen, men det finnes en mye enklere måte å løse ligningen på:

Dersom produktet av to faktorer skal bli null, må en av faktorene være null.

mn = 0 medfører at m eller n må være lik null, om utsagnet skal være riktig.

I eksemplet

(x + 1)(x – 2) = 0

betyr det at x+1 = 0 , eller at x – 2 = 0

Det gir løsningene x = -1 V x = 2

Problemet er redusert til løsninger av to enkle førstegradsligninger.

Faktorisering av andregradsuttrykk

ax² + bx + c er et generelt andregradsuttrykk. Ofte har man behov for å faktorisere uttrykket for å kunne forkorte og forenkle.

Man har følgende formel for faktorisering av andregradsuttrykk:

ax² + bx + c = a( x-x₁)(x-x₂)

Der x₁ og x₂ er løsninger av ax² + bx + c = 0

Sum og produkt av røtter

Man har følgende sammenhenger mellom sum og produkt av røtter (løsninger):

Dersom ax² + bx + c =0

er

               og

x₁ og x₂ er røtter (løsninger) i ligningen.

Dersom man anvender disse formlene og finner en ligning må man sjekke at den virkelig har løsninger.