|
kjegle En kjegle er definert av en plan lukket kurve og et punkt P, i rommet. Alle linjestykker fra P til den lukkede kurve kalles generatriser. Kjeglen består av alle generatriser og flaten som utspennes av den lukkede kurve, grunnflaten. Den lukkede kurve kalles ledekurve eller direktrise.
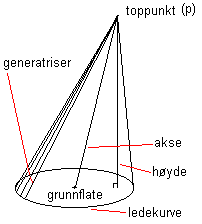
Figuren over viser en skjev kjegle. Dersom man tenker seg at man tar en rettvinklet trekant og roterer den rundt det ene katetet får man en rett sirkulær kjegle, som vist nedenfor. Grunnflaten i en kjegle kan ha forskjellig form, er ledekurven en sirkel kalles kjeglen sirkulær, er det en ellipse kalles den elliptisk.
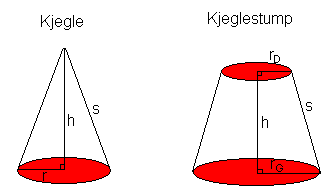
Volum av en kjegle er gitt ved : V = 1/3( πr2h)
Volumet av en kjegle er altså en tredjedel av en sylinder med tilsvarende grunnflate og høyde.
Overflaten av en kjegle er gitt ved: A = πr2 + πrs Det første av leddene er overflaten av grunnflaten (sirkelen). Det andre leddet er overflaten av selve "kremmerhuset". Det siste leddet fremkommer på følgende måte: Tenk deg at du klipper opp "kremmerhuset" i en rett linje langs s. Du får da en sirkelsektor der radien i sirkelen er s. Lengden av sirkelbuen er gitt ved 2πr, der r er radius i grunnflaten. Vi får da: πs2(2πr/2πs) = πrs.
Volumet av en kjeglestump er gitt ved:
V = πh/3(rG2 + rGrD + rD2)
|
 HJEM
HJEM